What Are the Different Types of Angles?An angle is a geometric figure that is formed when two lines meet each other at a point. Typically, we measure angles in degrees, and a complete turn of the angle measures up to 360 degrees. Straight angles are half of one whole turn and resemble a straight line the measure of these angles in 180 degrees. In simpler terms, the straight angle is the same as the angle formed by two rays drawn in the opposite direction. Right angles are one-quarter of the one whole turn and measure up to 90 degrees. These angles look like angles formed by a vertical line and a horizontal line. Acute angles are those angles that measure between 0 degrees to 90 degrees. Obtuse angles are those angles that measure between 90 degrees and 180 degrees. Angles that measure between a straight line (180 degrees) and a whole turn (360 degrees) are known as the reflex angle.
Basic Lesson
Guides students through solving Angle Word Problems. Two complementary angles measure x and 40 degrees.How many degrees are there in x?
View worksheetIntermediate Lesson
Demonstrates the concept of advanced skill while solving Angle Word Problems. Two complementary angles measure (3x+15) and (x+12) degrees. What is thevalue of x?
View worksheetIndependent Practice 1
A really great activity for allowing students to understand the concepts of the Angle Word Problems. Two vertical angles measure x and35 degrees. How many degrees are there inx?
View worksheetIndependent Practice 2
Students use Angle Word Problems in 20 assorted problems. The answers can be found below.
View worksheetHomework Worksheet
Students are provided with 12 problems to achieve the concepts of Angle Word Problems.
View worksheetSkill Quiz
This tests the students ability to understand Angle Word Problems.
View worksheetAnswer Key
Answers for all lessons and independent practice.
View worksheetBasic Lesson
Guides students through solving Types of Angles.
View worksheetIntermediate Lesson
Demonstrates the concept of advanced skill while Guides solving Types of Angles.
View worksheetIndependent Practice 1
A really great activity for allowing students to understand the concepts of the Types of Angles.
View worksheetIndependent Practice 2
Students use Types of Angles in 20 assorted problems. The answers can be found below.
View worksheetHomework Worksheet
Students are provided with 12 problems to achieve the concepts of Types of Angles.
View worksheetSkill Quiz
This tests the students ability to understand Types of Angles.
View worksheetAnswer Key
Answers for all the math worksheets and printables.
View worksheet
The measure of an inscribed angle is always half the measure of the central angle with the same endpoints. Since the diameter divides the circle into two equal parts, any angle formed by the two endpoints of a diameter and a third distinct point on the circle as the vertex is a right angle. Need some help figuring out how to work with angles in geometry? Look no further. From Ramanujan to calculus co-creator Gottfried Leibniz, many of the world's best and brightest mathematical minds have belonged to autodidacts. And, thanks to the Internet, it's easier than ever to follow in their footsteps (or just finish your homework or study for that next big test). Worksheets Math Grade 5 Geometry Estimating angles. How many degrees? Estimating angles. In these worksheets, students estimate angles based on the diagrams shown. These worksheets are printable pdf files. Similar: Classifying angles Classify and measure angles. Polygon Angles - Sample Math Practice Problems The math problems below can be generated by MathScore.com, a math practice program for schools and individual families. References to complexity and mode refer to the overall difficulty of the problems as they appear in the main program.
What Are Complementary, Supplementary, and Vertical Angles?
Complementary Angles - A pair of angles is said to be complementary when the sum of two angles adds up to be 90 degrees. The two angles in consideration form a right angle. For example, if we are given an angle that measures 40 degrees, the next angle has to be 50 degrees, if we have to make it a complementary angle. If you are given a complementary angle, you can be asked to calculate the measure of another angle. To solve this problem, you will need to figure out the measure of the next angle that, when added to the given angle, adds up to 90 degrees. You will have to subtract the given angle and subtract it from 90 degrees. For example, if you are given 55 degrees, you will subtract this angle from 90 degrees to get the measure of the next angle. Supplementary Angles - A pair of angles is said to be supplementary when the two angles add up to 180 degrees. Supplementary angles look like a straight line, which means two angles together will form a straight line. For example, two angles 65 and 115 degrees are supplementary as they add up to 180 degrees and form a straight line. Vertical Angles - When we have two lines intersecting each other, the angles present opposite to each other. We typically get four angles when two intersect each other, but the pair that measures the same is known as the vertical angle.
This fourth grade geometry lesson teaches the definitions for a line, ray, angle, acute angle, right angle, and obtuse angle. We also study how the size of the angle is ONLY determined by how much it has 'opened' as compared to the whole circle. The lesson contains many varied exercises for students.
| ||||
A line has no beginning point or end point. Imagine it continuing indefinitely in both directions. We can name a line using two points on it. This is line EF or line (note the arrowheads). | ||||
| ||||
What is an angle? Many people think that an angle is some kind of That point is called the vertex and the two rays are called the sides To name an angle, we use three points, listing the vertex in the middle. |
1. Write if each figure is a line, ray, line segment, or an angle, and name it.
a. _______________________ | b. _______________________ | c. _______________________ |
d. _______________________ | e. _______________________ | f. _______________________ |
2. a. Find the angle formed by the rays DE and DF.
How do we name it?
b. Find the angle formed by the rays CA and CE.
How do we name it?
c. What is BD? (a line, a line segment, or a ray)?
3. a. Draw two points, D and E. Then draw line DE.
b. Draw point Q not on the line.
c. Draw rays DQ and EQ.
d. Find angles EDQ and DEQ in your drawing.
| |||
If the angle opens up to a full | This angle is half of the full circle, Your two pencils (rays) are lying | This is one-fourth of the This is called the right | |
In each of these pictures the angle is opened more and more and keeps getting bigger. The arc of the circle is larger. These angles are acute angles, which means they are less than a right angle (less than 90°). Think of acute angles as sharp angles. If someone stabbed you with the vertex of an acute angle, it would feel sharp. | |||
Here's another way of thinking about angles. Think of a sun rising in the morning in the horizon, gradually getting higher, and traveling through the sky along an arc of a circle. | |||
| How big is the angle? It does not matter how long the sides of the angle are. Remember, they are rays, and rays go on indefinitely. But when we draw them on paper, we have to draw them as ending somewhere. The sides of the angle might even seem to have different lengths. That doesn't matter either. The size of the angle is ONLY determined by how much it has “opened” as compared to the whole circle. Think how big an arc of a circle the sides have drawn, as compared to a whole circle. | ||
|
4. Which angle is bigger?
|
|
| ||||||
|
|
|
5. a. Sketch three different
acute angles.
b. Sketch three different
obtuse angles.

c. Sketch a right angle
and a straight angle.
6. Label the angles as acute, right, obtuse, or straight. To help, make these angles with two pencils,
checking how much you need to open up the angle.
|
|
| |||
|
|
| |||
|
|
|
7. A triangle has three angles. In fact, the word tri-angle means a three-angled shape.
| Which of the triangles a, b, or c has one obtuse angle?
| a. | b. | c. |
8. (Optional) Make a geometry notebook where you write down each new term and draw a picture or
pictures that illustrate the term. Use colors and tidy writing. It is like your personal geometry
dictionary. You can also do any drawing problems from the lessons in it. Drawing and writing
yourself, instead of just reading, can help you remember the terms better!
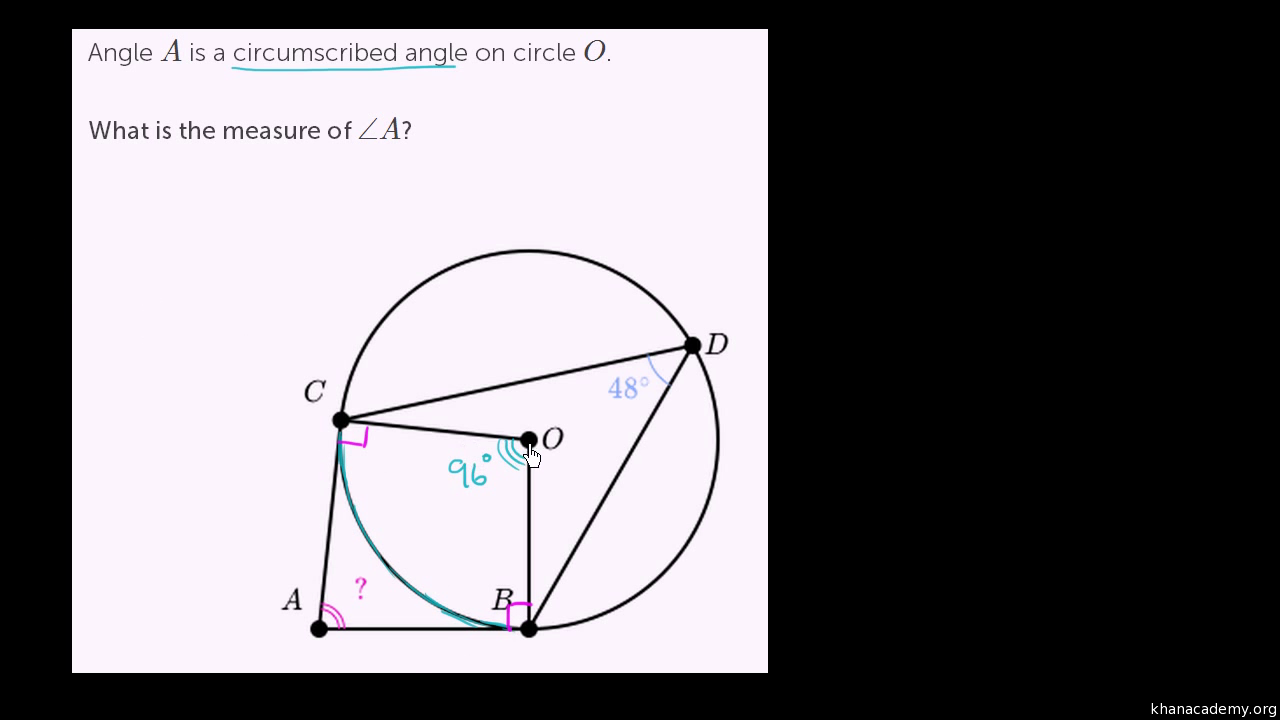
Math Problem Solvingcircles And Angles Theorem
| New Terms | ||
|
Grade 2 Math Problem Solving
This lesson is taken from Maria Miller's book Math Mammoth Geometry 1, and posted at www.HomeschoolMath.net with permission from the author. Copyright © Maria Miller.
Math Mammoth Geometry 1
A self-teaching worktext for 4th-5th grade that covers angles, triangles, quadrilaterals, cirlce, symmetry, perimeter, area, and volume. Lots of drawing exercises!
Download ($6.90). Also available as a printed copy.
Steps In Math Problem Solving
Math Problem Solvingcircles And Angles Worksheets
|
Solving Geometry Angle Problems
